Шо, опять магия? 
Часто анализируя большие массивы данных, а особенно данных с присущим им нестабильностям, волей-неволей задумываешься “Чо же тут вАще такое я вижу?”. Никогда не задавали себе этот вопрос? Я вот регулярно его себе задаю. И сегодня попробую вам выдать некоторые простые методики по обработке данных.
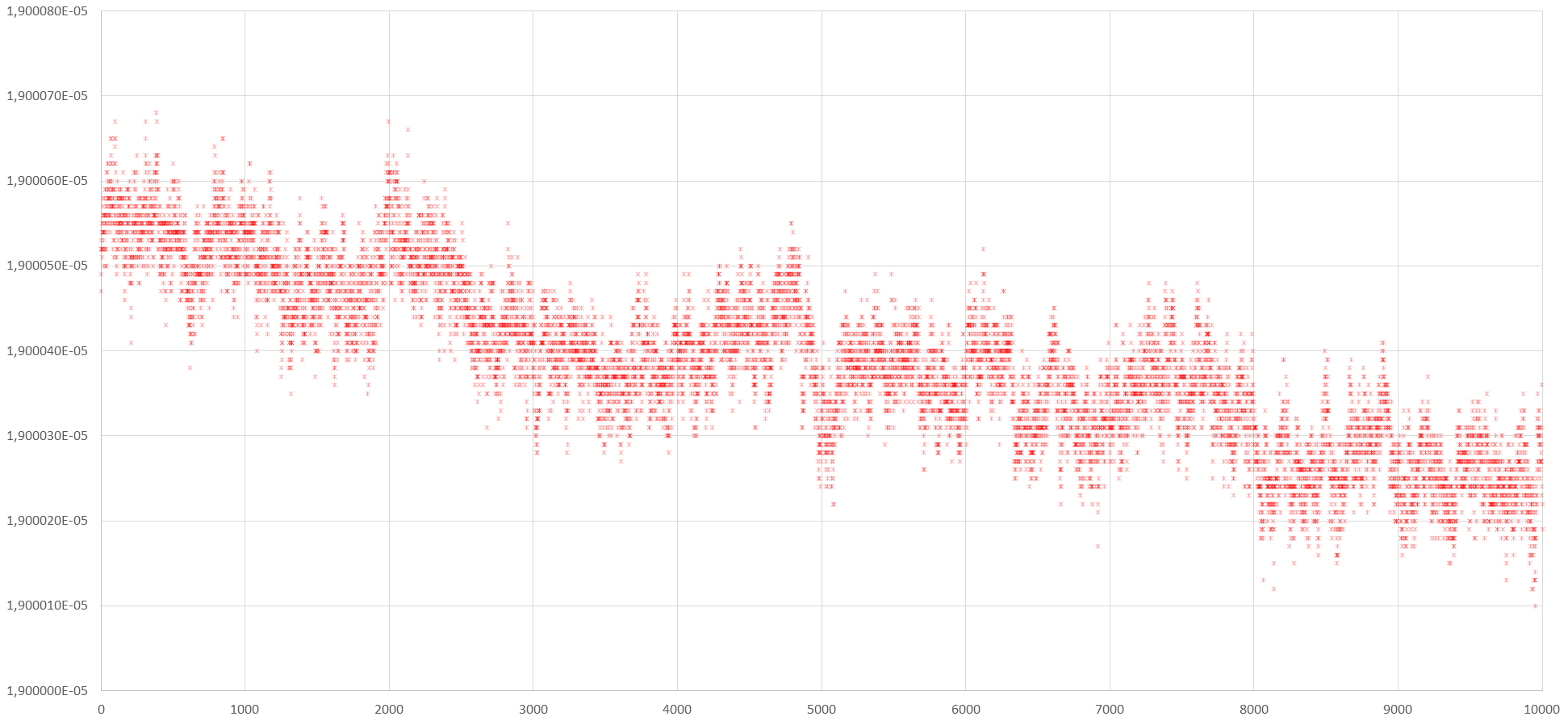
Начнем с того, откуда растут ноги. То что растут они из жопы, это очевидно, но постараемся оценить ее размер. Вот к примеру вы что-то самоотверженно измерили, как в прошлом материале стояла задача вычислить 3 точки для расчёта. Тут вы расчехлили свой стенд, протерли пыль, загрузили Raspberry Pi и получили массив данных 10 000 точек, протяженностью 5.5 часа, вот такой:
Но нам-то нужна всего одна точка, так какую-же из них выбрать? Ведь каждая из них, это показание вашего прибора в определенный момент времени, и все они это ваше измерение.
Первое что приходит на ум – высчитать среднее значение. И эта мысль не всегда верна. Проблема в том, что существует много разных видов статистических усреднений, основных из них по сути три “среднее арифметическое”, “медиана”, “мода”. И все они очень разные 
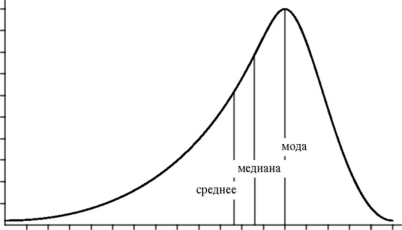
Если плотность значений(частоту повторения того или иного значения) считываемых с прибора представить в виде графика, то разница между этими стат. усреднениями будет видна.
Среднее арифметическое – его знают все, суммируем температуру по больнице, делим на количество пациентов, и получаем некую среднюю точку. У данного метода есть две проблемы:
- Если у кого-то из пациентов в ходе измерения лопнул градусник, и мы получили значение температуры стремящееся в бесконечность, то и средняя температура так-же будет стремится в бесконечность.
- Если какой-то небольшой процент градусников неисправен, он будет вносить серьезную погрешность в средний результат.
Ровно то-же самое часто происходит при измерении электрических параметров. Скажем ударили вы по столу в процессе измерений, на графике образовался пик, который сместил среднее в нежелательную сторону.
Медиана – более позитивная штука, это значение находящееся равно-удаленно от двух равных половин набора данных. В некоторых странах даже считается, что медиана более адекватна чем среднее. Она меньше реагирует на случайные всплески значений, хотя и надо признать такая реакция у нее все-же есть. Лишь малый процент данных при обработке массива по медиане теряется, но главный положительный момент – влияние редких и сильно удаленных точек от середины в значительной степени ослабляется.
Мода – по сути эта функция ищет экстремум графика плотности, выдавая в качестве ответа только самое часто встречаемое значение в массиве данных. Обладает огромным разрушительным действием и очень опасна Как пример, применив ее к набору данных выше, мы можем получить любое случайное число из этого массива, потому-что визуально зон резко-повешенной плотности значений там не наблюдается. Но если “исследователь” строго задался задачей поиска точки экстремума графика плотности, она очень полезна.
Результат обработки массива по этим трем функциям:
- Среднее: 1,9000382E-05
- Медиана: 1,9000380E-05
- Мода: 1,9000370E-05
Массив практически равномерен, по этому среднее и медиана очень близки, а вот мода куда-то отскочила…. вот гадина! Что в принципе и следовало доказать.
Для продолжения чтения рекомендую посмотреть(или пересмотреть) фильм “Игры разума” 2001-го года, чтобы проникнутся атмосферой того что сейчас будет происходить.
Зависимости и тренды
Самое интересное начинается, если задумываться о природе тех или иных нестабильностей или шумов. Это я-бы сказал самое интересное во всех моих экспериментах, и именно поиск причин нестабильности и их как таковых. Все это требует все-те горы лаб. оборудования которые представлены в соответствующем разделе бложика. Поскольку просто “что-то измерить” это не интересно… интересно добраться до самого дна измеряемой величины и определить ее параметры.
Как в примере выше, мы видим что ток через меру куда-то стремительно уменьшается. Встает несколько вопросов: насколько? куда? почему? обратим ли этот процесс? а если он продолжится мера въебет?…. и т.п.
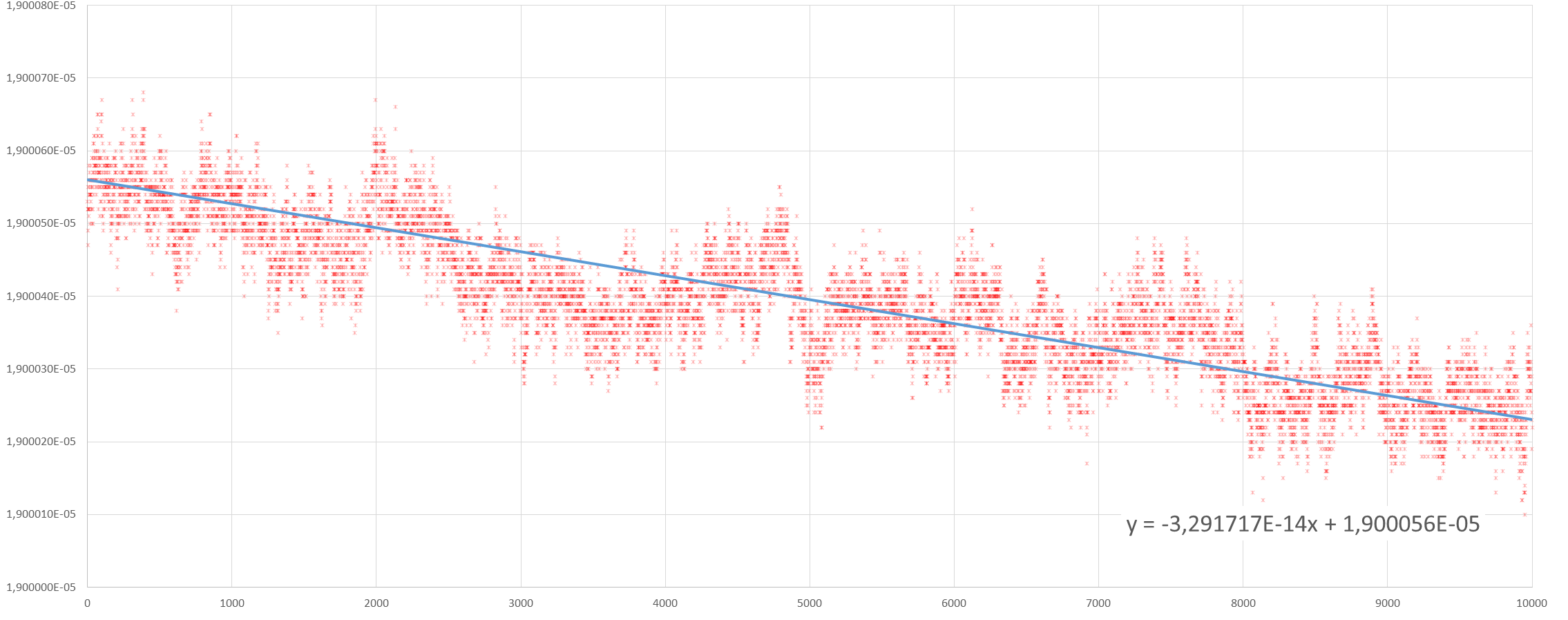
На вопросы “куда она плывет и насколько быстро?” зачастую отвечают функции построения трендов:
В данном случае тренд простой и имеет линейную характеристику выражаемую формулой:
y = -3,291717E-14x + 1,900056E-05
Где первый аргумент это коэффициент скорости, а второй точка начала отсчета.
Зная что один X равен времени ровно 2 секунды, можно вычислить временную характеристику тренда в относительной величине:
1 / ( 1,900056E-05 / -3,291717E-14 ) = -1,73243E-09
-1,73243E-09 * 1E6 = -0,001732432 ppm/на отсчет
-0,001732432 / 2 сек = -0,000866216 ppm/сек
Кажется сначала, что величина пренебрежимо мала, но это не так. Если ее экстраполировать на интервал в 1 сутки:
-0,000866216 * 86400 = -74,8 ppm/день
А это уже весьма большое значение, превышающее допуск этой меры. Ок, мы нашли некоторый тренд, выяснили его направление, его скорость -74,8 ppm/день, и она очень высокая. И тут-же понимаем, что где-то здесь кроется проблема, этого не может быть, т.к. за 39 лет мера не вышла из своего допуска, а измерение нам говорит, что менее через сутки она полностью въебет!!! ААААА палундра! срочно все выключаем и начинаем думать!!! Параллельно пересматривая “игры разума”…. И начинаем искать связи и зависимости!
Что может повлиять на результат такого измерения:
- Нестабильность напряжения питания меры.
- Нестабильность измерителя тока.
- Нестабильность температуры меры.
- Самонагрев катушки.
- Эффекты старения.
- Скорость ветра на марсе.
Самый простой способ нахождения проблемы – исключить влияющие факторы методом исключения и экспериментом.
- Нестабильность питания я обычно предпочитаю не исключать, а компенсировать ее математически измеряя ее в процессе эксперимента.
- Нестабильность температуры уберем с помощью термокамеры.
- Самонагрев если прикинуть, (190 В / 10 МОм) * 190 В = 3.6 мВт на 2 килограмма массы меры, пренебрежимо мал с учетом активной конвекции в термобоксе.
У меня закралось сомнение, что всему виной стрессовые факторы, такие как всплески температуры и протекание тока через катушку. Если исключить все доступные факторы и провести стресс тест, это можно попробовать доказать.
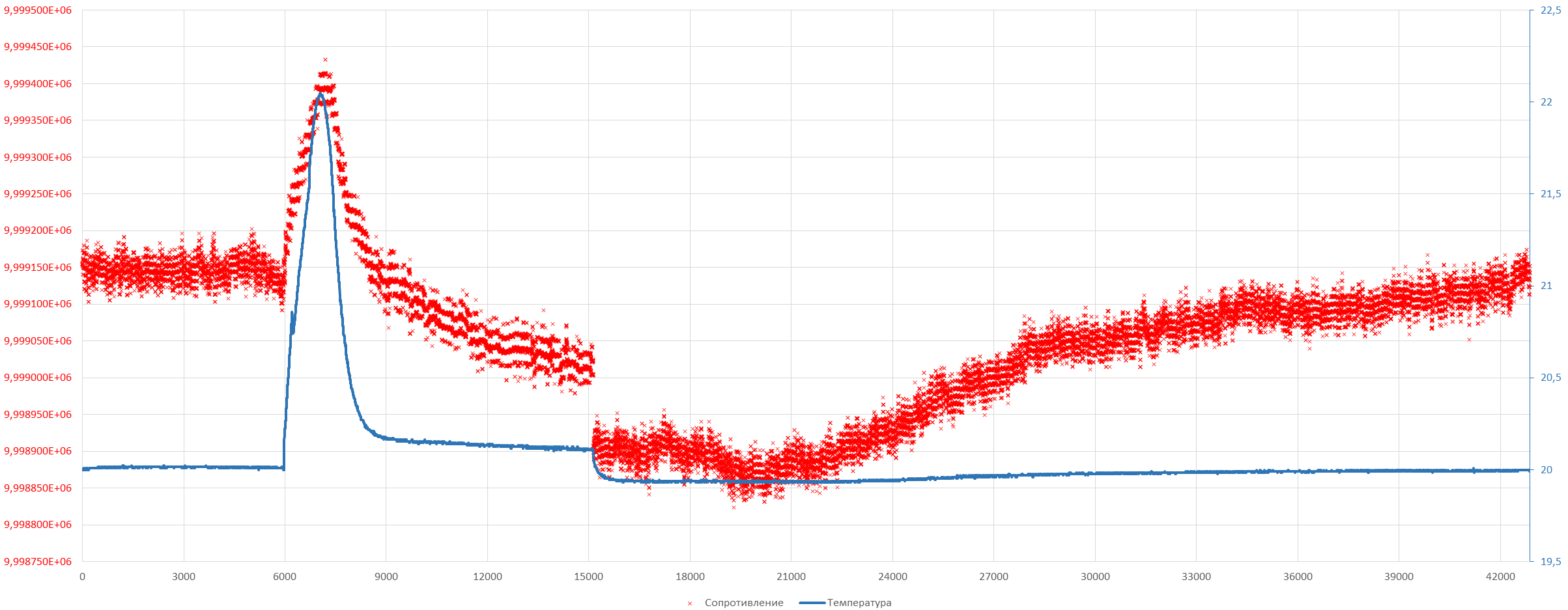
Получается простой эксперимент: ставим катушку в термобокс, контролируем напряжение питания пересчитывая его и ток в сопротивление, измеряем начальное сопротивление на маленьком напряжении 10В, затем устраиваем стресс катушке, обеспечивая бросок температуры и длительную подачу напряжения 510В на катушку, сразу после этого возвращаем начальные условия и проверяем есть-ли эффект релаксации.
- Начальные условия в точке 0: температура воздуха 20°C, напряжение питания 10 В.
- На точке 6000 напряжение было увеличено до 510В а по температуре был эмитирован всплеск.
- На точке 15000 напряжение и температура возвращены к начальным условиям 20°C и 10 В.
Поскольку стрессу подвергалась только мера, а не приборы измеряющие ток и напряжение, то график наглядно показывает что стрессовые условия, даже не смотря на то, что они в рамках рабочих характеристик катушки – негативно влияют на ее характеристики. При снятии стрессовых условий требуется более 16 часов релаксации(один отсчет по оси X=2 секунды).
Так-же видно, что датчик внутри катушки смог зафиксировать самонагрев на +0.11°C(хвала датчикам TI TMP117) внутреннего пространства меры. Это видно по спаду температуры в точке 15000, когда тестовое напряжение резко упало с 510 до 10 вольт. Не удивительно, ведь в этом эксперименте тепловыделение на мере составило уже 26 мВт.
Повторение эксперимента показывает, что в зависимости от величины и комбинации стрессовых факторов, скорость дрейфа сопротивления, его направление и время релаксации может меняться.
Из этого простого эксперимента я делаю вывод, что для точных измерений эти катушки(Р4013, Р4023, Р4033) не желательно эксплуатировать на высоких тестовых напряжениях и подвергать их стрессам. А перед и после измерений желательно релаксировать их 1-2-е суток. А то, что на катушку даны данные по номинальному напряжению 550В и придельному 1500В, к этому стоит относится скептически.
Резюме
Мат обработка и крейзи эксперименты – это не только весело, но и порой вылезает такое… что диву даёшься
Короче говоря: экспериментируйте, анализируйте, считайте, ищите зависимости! Я не призываю всем становится экспертами по мат. статистике, но минимальный набор навыков, пусть даже чисто интуитивных, приходится так или иначе получать.
В глубинные проблемы я не вдавался, думаю пока с вас и этого хватит… 