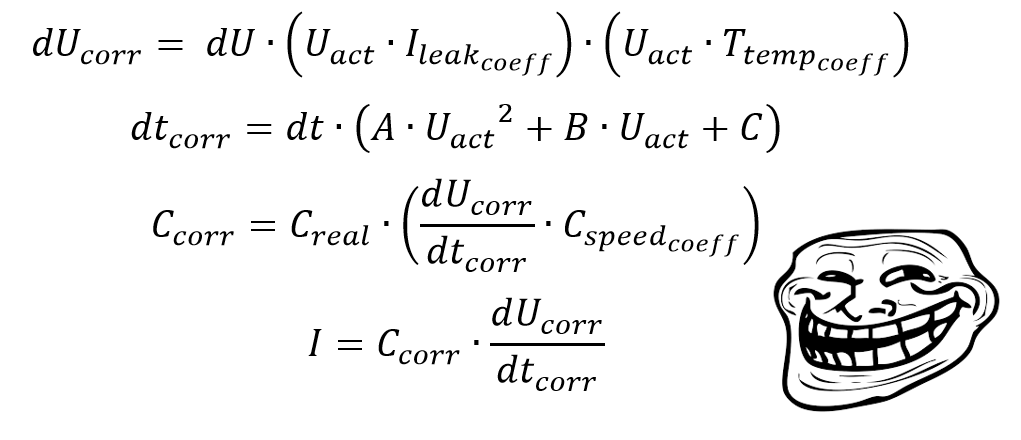
 Материал будет дан своими словами, с упрощением в части терминологии, по этому будет не полностью соответствовать общепринятым понятиям, но должен отчетливо донести суть.
Материал будет дан своими словами, с упрощением в части терминологии, по этому будет не полностью соответствовать общепринятым понятиям, но должен отчетливо донести суть.
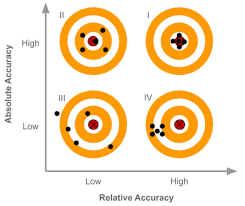
Абсолютная погрешность – Разность Δ между измерением какой-то величины, и ее истинным значением. К примеру при измерении напряжения, это разность между тем, что отображается на экране мультиметра, и реальным(идеально точным) напряжением которое действительно подается на вход мультиметра. То есть разница показания мультиметра с эдаким абсолютно идеальным сферическим конем в вакууме, который точнее самого точного эталона на планете земля(читай теоретическим определением вольта).
Относительная(как частный случай дрейф) погрешность – Разность Δ между несколькими измерениями какой-то величины, при условии что измеритель абсолютно стабилен. Пример, при измерении напряжения на протяжении нескольких часов, мы получаем набор данных с некоторым разбросом показаний, если стабильность мультиметра значительно лучше чем измеренный разброс измерений, мы можем вычислить по этому массиву данных, собранных за часы измерения этот разброс Δ.
При высокой точности измерения относительной погрешности и одновременном измерении совокупных условий измерения, часто возможно найти связи дрейфа и какого-то совокупного условия измерения, и выразить это формулой.
Но теория скучна и абсолютно бесполезна, если ее оторвать от практики. По этому наиболее важно то, как мы можем применить ее на практике. А практиковаться мы будем естественно с ГЛИН-ом 
Рассмотрим основополагающую формулу синтеза тока ГЛИН-ом:
Чуть посложнее получилась, чем те что я писал ранее, не так ли? Ну такое случается, когда теория разбивается о гранит реальности 😀
Если мы просто перенесем единицу напряжения путем измерения напряжения опоры LM399AH, единицу емкости компарированием относительно меры емкости, и частоту опорного генератора путем ее измерения относительно GPSDO, то нам нечем будет закрыть кучу всех этих коэффициентов линейной и полиномиальной коррекции. Для их определения необходимо определить дрейфы и прочие относительные погрешности синтеза формулы:
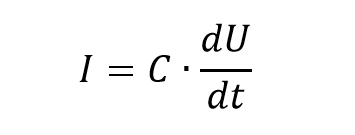
А без корректирующих коэффициентов линейности, температурных коэффициентов напряжения, коэффициентов зависимости утечки конденсатора от напряжения, и прочих, в сухом остатке мы легко можем получить:
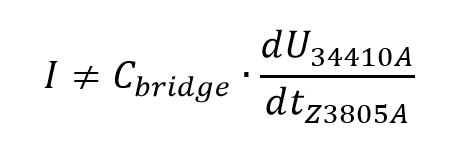
- Абсолютная погрешность моего мультиметра Agilent 34410A по напряжению 10В составляет менее 40ppm за 3 года.
- Абсолютная погрешность частоты моего GPSDO HP Z3805A составляет менее 0.01ppb.
- Абсолютная погрешность переноса единицы емкости в моей лабе, на данный момент составляет менее 250ppm.
Простая калькуляция дает максимальную абсолютную погрешность синтеза тока 290ppm.(то что данная калькуляция, простое суммирование всех явных погрешностей переноса единиц, в корне не верный подход, я в данном материале опускаю)
И видимо по этой причине неоднократно мне высказывали мнение, что запредельные стабильности блока времени в ГЛИН избыточны, потому-что люди сравнивают сумму 290ppm абсолютных погрешностей емкости и напряжения с погрешностью дрейфа времени 0.001ppm обеспечиваемой ГЛИНом. При первом приближении, да это так! Но теперь давайте рассмотрим вопрос детальнее.
Нам надо определить коэффициенты полинома коррекции линейности “Ax2+Bx+C”, для этого я беру мультиметр Keithley DMM6500 который типично обеспечивает линейность шкалы -10В….+10В лучше 1ppm.
И стабильность измерения напряжения лучше 1ppm на протяжении всего цикла измерения . Опора напряжения в ГЛИН-е так-же обеспечивает стабильность лучше 1ppm, на протяжении всего цикла измерения.
Это означает, что для того, чтобы достоверность определения линейности функции деления dU/dt сохранилась, необходимо чтобы часть “t” формулы имела как минимум схожую стабильность, а лучше превосходящую.
Если мы рассмотрим вариант применения в качестве опоры времени простой кварцевый резонатор, то он обеспечит стабильность максимум в десятки ppm, на протяжении всего цикла измерений, что недостаточно.
Если применить хороший термокомпенсированный кварцевый резонатор(TCXO), то стабильность составит уже около 0.5….0.1ppm, в лучшем случае. Что достаточно, но поскольку эта стабильность сравнима со стабильностью всех остальных частей, она проссумируется и ощутимо увеличит относительную погрешность.
Если применить термостатированный кварцевый резонатор(OCXO), стабильность которого около 0.001ppm, вклад стабильности в общую ошибку измерения линейности будет уже пренебрежимо мал.
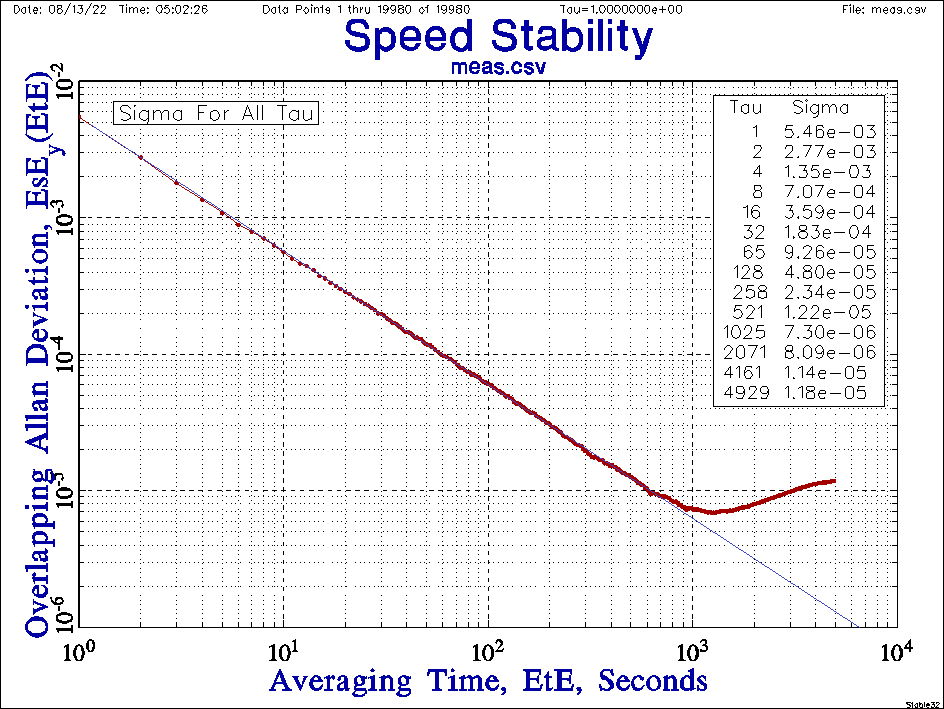
В результате, после фильтрации шумов вызванных множеством разных эффектов измерительного тракта, можно получить данные по линейности скорости ЛИН, стремящейся к 1ppm. Хотя с первого взгляда, одной ppm-кой там и не пахнет:
Но на этом графике я вижу зависимость, и девиация Аллана так-же показывает надежды на возможность приближения к заветной ppm-ке.
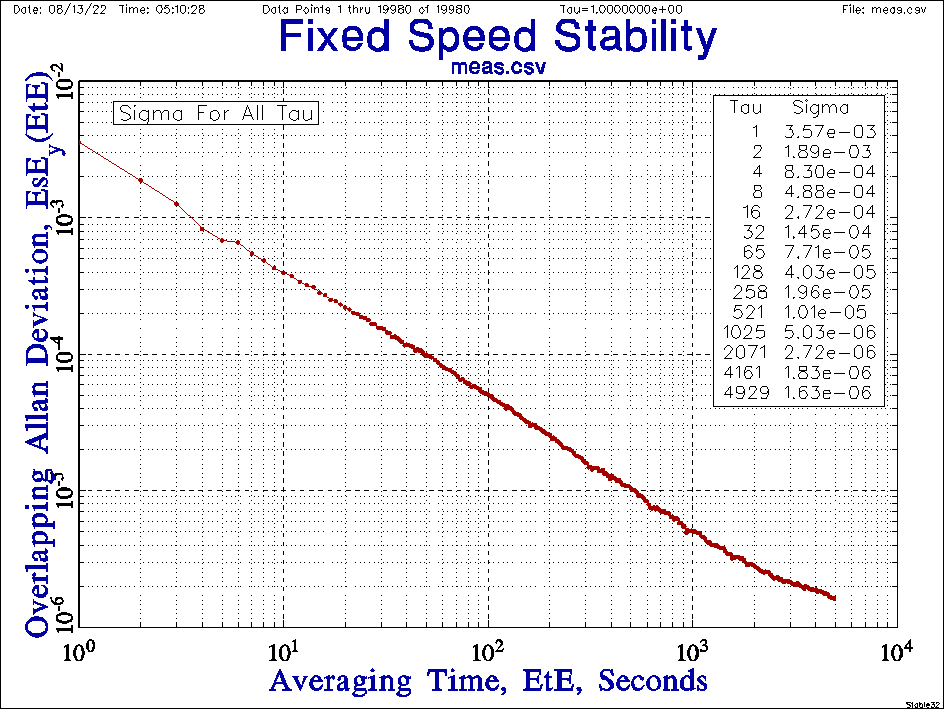
Если вычислить корректирующие полиномиальные коэффициенты с максимально возможной относительной точностью, стремящейся в суб-ppm-ную область. То, после программирования в ГЛИН коэффициентов коррекции линейности через полином 2-го порядка, получаем уже график девиации Аллана по скорости, значительно приближенный к идеальному.
Если-бы дрейф времени на протяжении цикла измерения был-бы десятки-сотни ppm, как рассматривалось в самом начале, вычислить коэффициенты коррекции для приближения линейности к нескольким ppm было-бы попросту невозможно.
Характерной особенностью данных графиков является шум, сильно напоминающий смесь фазового фликкер-шума и белого шума (тау-1) мультиметра, с четко выраженным наклоном 10дБ на декаду. Если шум был бы меньше, удалось бы достичь еще лучших результатов. Типично, мультиметры этот шум в значительной степени давят, когда речь идет о измерении постоянного напряжения, но при измерении изменяющегося процесса, этот шум они подавить не могут, так как их шкалу напряжения растягивает шкала времени. Это связанно с разрядностью мультиметра, и с тем что мы измеряем не “U” а “dU/dt”. К примеру при вычислении ошибки скорости 1мВ/c в интервале 100 секунд, мультиметру на диапазоне 10В надо зафиксировать разницу напряжений 100мВ. При разрешении 6.5 разряда хороший мультиметр может измерить разницу между точками 100мВ с разрешением лучше 1мкВ, что есть 0.001% от величины. Что мы и наблюдаем на графике девиации Аллана, при базовой скорости 1мВ/c девиация Аллана в точке 100 сек, составляет примерно 1мВ/c*6*10-5=60нВ/c. И это абсолютный максимум, который вообще можно вытащить из очень-очень хорошего 6.5 разрядника, стабильность и разрядность которого превосходит олдскульных представителей 6.5-разрядного семейства.
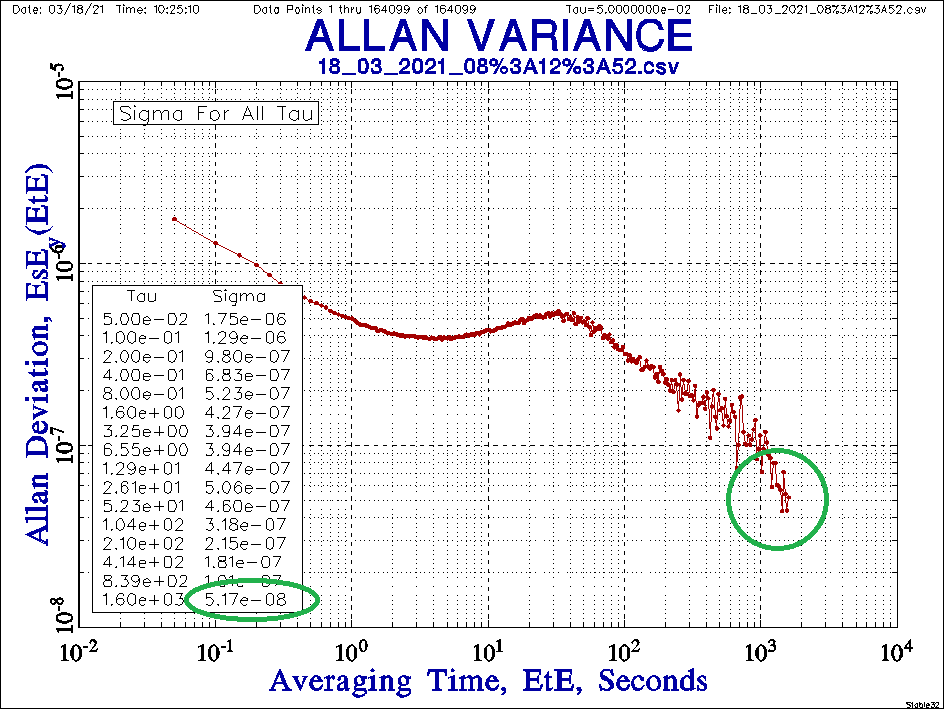
Вытащить с него что-то лучшее просто нереально, ибо при времени измерения >2 тыс. секунд, при котором формировался график, девиация его дрейфа нуля как раз составляет 1В*5.1*10-8=51нВ.
По этому в лабораториях принято применять HP 3458A, который может вытащить немного большее разрешение между двумя точками и имеет чуточку лучшие показатели девиации при длительных измерениях(>2 тыс.сек.).
И это все тоже относительные характеристики(стабильность).
Причем замечу, что все эти измерения практически толерантны к абсолютной погрешности, но очень чувствительны к дрейфовой(относительной) погрешности. А она обычно во много раз лучше абсолютной. И только благодаря этому возможно измерение с такой точностью.
Теперь попробую донести суть, и надеюсь станет более понятно – дрейф это в сути своей стабильность. Если абсолютная погрешность показывает возможную ошибку относительно идеальной величины, то дрейф часто может показать стабильность такой ошибки во времени, или относительно какого-то параметра. И измерения базирующиеся на компонентах и приборах с малым дрейфом позволяют определить и помочь компенсировать проблемы стабильности.
Именно из за необходимости высокой стабильности ГЛИН, их оценивают не только по абсолютной погрешности, но так-же ключевым параметром в ряде лабораторий является RSD Relative Standard Deviation (Относительная Стандартная Девиация). Которая тоже вычисляется исключительно в относительных величинах дрейфа на протяжении полного цикла ГЛИНа. Я ориентируюсь на данные PTB(Physikalisch-Technische Bundesanstalt), чей ГЛИН обеспечивает RSD 1.3E-5.
Резюмирую, что можно получить в моем случае благодаря высокой точности дрейфовых(относительных) измерений:
- Высокую стабильность прибора в рамках цикла измерений.
- Высокую относительную точность синтеза формулы.
- Высокую повторяемость измерений.
- Возможность применять ГЛИН для задач относительного компарирования двух емкостей в области инфра-низких частот, с точностью значительно превышающей абсолютную погрешность переноса базовых единиц системы СИ.
- Возможность создания мостовых компараторов сверхмалых токов из нескольких ГЛИН-ов, с точностью значительно превышающей абсолютную погрешность переноса базовых единиц системы СИ.
Вычисление абсолютной-же погрешности лишь позволят оценить ошибку синтеза тока, но не дает данных о стабильности. А самое основное веселье, это какраз относительные измерения